Python
(Numpy: Polyval, Polyder)
Python (Numpy: polyval)
안녕하세요, 제 블로그는 제가 공부하면서 어려웠던 부분에 대해서 정리하고 공유하는 블로그 입니다.
오늘은 다시 Polyval 함수에 대해서 알아보겠습니다.
그럼 시작해보겠습니다.
1. polyval
code:
numpy.polynomial.polynomial.polyval(x, c, tensor=True)
description:
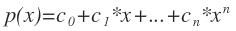
x : 입력할 값 (scalar 값, tuple, list 가능)
c : 계수 또는 coefficient, 이하 coeff (array 형태)
x가 스칼라 값이고, coeff 가 1차원 배열일 경우 위의 p(x) 함수와 같은 형태가 된다.
tensor=True * 아래에서 다시 언급
일단 코드를 보며 이해를 해봅시다.
(좀 복잡해야 어떻게 활용해야 할지 알 수 있기 때문에 x, coeff 모두 array 형태로 대입해 보겠습니다.)
In [19]: x
Out[19]:
array([[1, 2],
[3, 4]])
In [20]: coeff
Out[20]:
array([[1, 2, 3],
[4, 5, 6]])
In [21]: polyval(x, coeff)
Out[21]:
array([[[ 5., 9.],
[ 13., 17.]],
[[ 7., 12.],
[ 17., 22.]],
[[ 9., 15.],
[ 21., 27.]]])
coeff 이 녀석이 헷갈리는데, coeff가 1차원 배열이 아닐 때에는 무조건 ,를 기준으로 왼쪽(배열)부터 오른쪽(배열) 끝까지 각 배열이 요소 하나씩 보면 됩니다.
위의 식에서 coeff = [[1,2,3] , [4,5,6]] 로 정의를 했는데 coeff는 (1, 4), (2,5), (3, 6) 로 짝을 이루어서 적용되게 됩니다.
만약 [[1,2,3], [4,5,6], [7,8,9]] 라면 coeff는 (1,4,7), (2,5,8), (3,6,9) 가 되었겠죠.
위의 코드를 정리하면
x=1 , coeff=(1, 4)
x=2 , coeff=(1, 4)
x=3 , coeff=(1, 4)
x=4 , coeff=(1, 4)
x=1 , coeff=(2, 5)
x=2 , coeff=(2, 5)
x=3 , coeff=(2, 5)
x=4 , coeff=(2, 5)
x=1 , coeff=(3, 6)
x=2 , coeff=(3, 6)
x=3 , coeff=(3, 6)
x=4 , coeff=(3, 6)
와 같이 계산이 되는 것을 알 수 있습니다.
tensor=True : x의 모든 값에 대해서 coeff를 적용
tensor=False: x를 brodcast 하게 coeff에 적용
예를 들어서, 아래와 같이 x, coeff가 주어졌다고 하자
In [33]: x
Out[33]: [[1, 2], [3, 4]]
In [34]: coeff
Out[34]:
array([[1, 2],
[3, 4],
[5, 6]])
tensor=True 일때,
In [35]: polyval(x, coeff)
Out[35]:
array([[[ 9., 27.],
[ 55., 93.]],
[[ 12., 34.],
[ 68., 114.]]])
- x = 1,2,3,4 일때 coeff (1,3,5) 적용 -> 2X2 배열 출력
- x = 1,2,3,4 일때 coeff (2,4,6) 적용 -> 2X2 배열 출력
tensor=False 일때,
In [36]: polyval(x, coeff, tensor=False)
Out[36]:
array([[ 9., 34.],
[ 55., 114.]])
- x = 1 일때, coeff (1,3,5) 적용 -> 9
- x = 2 일때, coeff (2,4,6) 적용 -> 34
- x = 3 일떄, coeff (1,3,5) 적용 -> 55
- x = 4 일때, coeff (2,4,6) 적용 -> 114
위의 결과를 보면 알 수 있듯이 tensor가 False 이면 array x의 각 element에 해당되는 위치의 coeff가 brodcast 하게 적용 된다.
2. polyder
code:
numpy.polynomial.polynomial.polyder(c, m=1, scl=1, axis=0)
description:
c : 계수 또는 coefficient, 이하 coeff (array 형태)
m=1 : 미분 횟수 (기본 1)
scl=1 : 선형변환시 계수
axis=0 : 미분 방향
주어진 c(coefficient) 로 이루어진 다항식을 한번 미분한 후 계수를 출력하는 함수
coeff
Out[60]:
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
np.polynomial.polynomial.polyder(coeff)
Out[61]:
array([[ 2., 3.],
[ 8., 10.],
[ 18., 21.],
[ 32., 36.]])
아래와 같은 다항식이라고 생각하고 1번 미분이 된다.
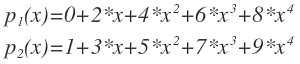
m=1(기본), m=2 또는 그 이상일 경우
np.polynomial.polynomial.polyder(coeff, m=1)
Out[68]:
array([[ 2., 3.],
[ 8., 10.],
[ 18., 21.],
[ 32., 36.]])
np.polynomial.polynomial.polyder(coeff, m=2)
Out[69]:
array([[ 8., 10.],
[ 36., 42.],
[ 96., 108.]])
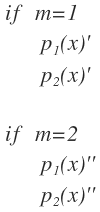
scl=1(기본): x 일 때
scl=n 일 경우 : x대신 nx 일 때
np.polynomial.polynomial.polyder(coeff, scl=1)
Out[70]:
array([[ 2., 3.],
[ 8., 10.],
[ 18., 21.],
[ 32., 36.]])
np.polynomial.polynomial.polyder(coeff, scl=2)
Out[71]:
array([[ 4., 6.],
[ 16., 20.],
[ 36., 42.],
[ 64., 72.]])
np.polynomial.polynomial.polyder(coeff, scl=3)
Out[72]:
array([[ 6., 9.],
[ 24., 30.],
[ 54., 63.],
[ 96., 108.]])
위와 같이 (nx)를 미분했기 때문에 chain rule에 의해 f(nx)'=n*f'(nx) 가 된다.
m과 scl을 같이 사용했을 경우
np.polynomial.polynomial.polyder(coeff, m=1, scl=1)
Out[74]:
array([[ 2., 3.],
[ 8., 10.],
[ 18., 21.],
[ 32., 36.]])
np.polynomial.polynomial.polyder(coeff, m=2, scl=3)
Out[75]:
array([[ 72., 90.],
[ 324., 378.],
[ 864., 972.]])
2번 미분하고 x대신 3x를 집어 넣었을 경우
- 1번 미분시 (3x):
[ 2., 3.],
[ 8., 10.],
[ 18., 21.],
[ 32., 36.]
에서 3x 속미분 한번
[ 6 (2*3), 9 (3*3)],
[ 24 (8*3), 30 (10*3],
[ 54 (18*3), 63 (21*3)],
[ 96 (32*3), 108 (36*3)]
- 2번 미분시 (3x):
[ 8., 10.],
[ 36., 42.],
[ 96., 108.]]
에서 3x 속미분 두번
[ 72 (8*3^2), 90 (10*3^2)],
[ 324,(36*3^2) 378 (42*3^2)],
[ 864,(96*3^2) 972 (108*3^2)]
axis=0(기본), axis=1 의 차이점
np.polynomial.polynomial.polyder(coeff, axis=0)
Out[82]:
array([[ 3., 4., 5.],
[ 12., 14., 16.]])
np.polynomial.polynomial.polyder(coeff, axis=1)
Out[83]:
array([[ 1., 4.],
[ 4., 10.],
[ 7., 16.]])
둘의 미분하는 방향이 다르다.
axis=0 은 종방향으로 계수를 생각하여 미분
axis=1 은 횡방향으로 계수를 생각하여 미분
오늘은 여기까지 polyval와 polyder 함수에 대해서 알아보았습니다.
이제 개강이네요.. 슬슬 정리할 것도 많아 지고 공부해야 할 것도 많아 질 것 같습니다.
